1. Hàm đệ quy (recursive function) là gì?
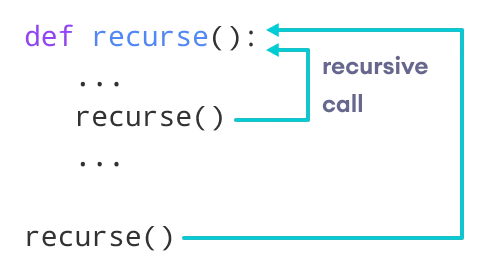
Một hàm gọi chính nó được gọi là hàm đệ quy. Kỹ thuật lập trình này gọi là đệ quy.
def recurse():
...
recurse()
...
recurse()
Lưu ý: Không thể để hàm gọi hàm liên tục, vô hạn được. Để ngăn chặn đệ quy vô hạn, thường sử dụng câu lệnh if. Tức là, mọi hàm đệ quy phải có một điều kiện dừng đệ quy, tránh hàm gọi hàm vô hạn.
Trình thông dịch Python giới hạn độ sâu của đệ quy (depths of recursion) để giúp tránh đệ quy vô hạn, dẫn đến tràn ngăn xếp (stack). Theo mặc định, độ sâu tối đa của đệ quy là 1000. Nếu vượt qua giới hạn sẽ dẫn đến lỗi RecursionError. Ví dụ:
def recursor():
recursor()
recursor()
Kết quả
Traceback (most recent call last):
File "c:\python-examples\sumPython.py", line 3, in <module>
recursor()
File "c:\python-examples\sumPython.py", line 2, in recursor
recursor()
File "c:\python-examples\sumPython.py", line 2, in recursor
recursor()
File "c:\python-examples\sumPython.py", line 2, in recursor
recursor()
[Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceeded
Chương trình Python tính giai thừa minh họa hàm đệ quy
Tính giai thừa của n: S(n) = n! = 1*2*…*(n-1)*n
Ta thấy S(n) = S(n-1)*n. Vậy thay vì tính S(n) ta sẽ đi tính S(n-1). Tương tự tính S(n-2), …, S(2), S(1), S(0) = 1.
#Factorial of n = 1*2*3*...*n
def factorial(n):
if (n > 1):
return n * factorial(n - 1)
else:
return 1
n = int(input("Enter a non-negative number: "))
while(n<=0):
n = int(input("Enter a non-negative number: "))
result = factorial(n)
print("Factorial of", n, "=", result)
Kết quả
Enter a non-negative number: 4
Factorial of 4 = 24
Hàm đệ quy def factorial(n) trên hoạt động như sau:
def factorial(n):
if (n > 1):
return n * factorial(n - 1)
else:
return 1
Khi nhập n = 4, gọi hàm result = factorial(n); tức là result = 4 * factorial(3). Hàm factorial(3) = 3 * factorial(2). Hàm factorial(2) = 2 * factorial(1). Mà khi n = 1 (không thỏa điều kiên if (n > 1)) thì return 1 tức là factorial(1) = 1.
Do đó, result = factorial(n) = 4*3*2*1 = 24.
2. Chương trình xuất dãy số fibonacci sử dụng hàm đệ quy
Dãy Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 và 1. Các phần tử sau đó được thiết lập theo quy tắc mỗi phần tử luôn bằng tổng hai phần tử trước nó. Công thức truy hồi của dãy fibonacci có dạng: f(n) = f(n-1) + f(n-2) với f(0) = 0, f(1) = 1.
Khi tính f(n) với n > 1 phải dựa vào 2 số fibonacci trước đó. Bài toán này có thể dùng hàm đệ quy như sau:
def fibonacci(x):
if((x==1) or (x==0)):
return x
else:
return fibonacci(x-1) + fibonacci(x-2)
i=0
x = int(input("Enter the number of terms of series : "))
while(x<=1):
x = int(input("Enter the number of terms of series : "))
print("Fibonacci Series : ")
while i < x:
print(fibonacci(i), end=' ')
i = i + 1
Kết quả
Enter the number of terms of series : 5
Fibonacci Series :
0 1 1 2 3
3. Ưu và nhược điểm của hàm đệ quy
Ưu điểm:
– Giúp code ngắn hơn và rõ ràng hơn.
– Một nhiệm vụ phức tạp có thể được chia thành các bài toán con đơn giản hơn bằng cách sử dụng đệ quy.
Nhược điểm:
– Việc gọi hàm liên tục sẽ làm khởi tạo các biến cục bộ trong hàm một cách liên tục và gây tốn bộ nhớ.
– Quá trình xử lý tốn nhiều thời gian hơn.
– Khó debug để tìm ra lỗi.