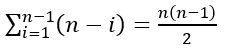1. Giới thiệu bài toán sắp xếp
Cho danh sách có n phần tử a0, a1, a2,…,an-1. Bài toán sắp xếp là quá trình xử lý các phần tử trong danh sách để đặt chúng theo một thứ tự thỏa mãn một số tiêu chuẩn nào đó dựa trên thông tin lưu tại mỗi phần tử.
Ví dụ, sắp xếp điểm trung bình theo thứ tự tăng dần, sắp xếp danh sách sinh viên tăng theo tên,..
Khái niệm cặp nghịch thế
Cho danh sách có n phần tử a0, a1, a2,…,an-1. Giả sử muốn sắp xếp danh sách a theo thứ tự tăng dần. Nếu i < j và ai > aj thì ai và aj là cặp nghịch thế.
Ví dụ:
a[0]=34, a[1]=3 là cặp nghịch thế.
Nguyên tắt sắp xếp danh sách (giả sử theo thứ tự tăng), ta tiến hành triệt tiêu tất cả các nghịch thế trong danh sách bằng cách hoán vị (hiểu đơn giản là đổi chổ các phần tử trong danh sách).
Một số thuật toán sắp xếp thường dùng
- Đổi chổ trực tiếp (Interchange Sort)
- Chọn trực tiếp (Selection Sort)
- Sắp xếp nổi bọt (Bubble Sort)
- Chèn trực tiếp (Insertion Sort)
- Quick Sort
2. Thuật toán sắp xếp đổi chổ trực tiếp
Ý tưởng
Xuất phát từ phần tử đầu danh sách, tìm tất các các cặp nghịch thế chứa phần tử này. Triệt tiêu chúng bằng cách đổi chỗ 2 phần tử trong cặp nghịch thế. Lặp lại xử lý trên với phần tử kế tiếp trong danh sách.
Các bước tiến hành thuật toán khi sắp xếp tăng dần
Bước 1: i = 0;//Bắt đầu từ đầu dãy
Bước 2: j=i+1;//Tìm a[j] < a[i] với j > i.
Bước 3:
Khi j < n thì kiểm tra: nếu a[j] < a[i] thì hoán vị a[j] và a[i].
Gán j=j+1; rồi thực hiện lại bước 3.
Bước 4: i=i+1; nếu i < n-1 thì lặp lại bước 2, ngược lại -> Dừng.
Minh họa thuật toán sắp xếp Interchange Sort
Cài đặt thuật toán sắp xếp đổi chổ trực tiếp với C++
#include <iostream>
using namespace std;
void Interchange_Sort(int a[], int n){
int i,j;
for(i=0; i<n-1; i++){
for(j=i+1; j<n; j++){
if(a[i]>a[j]){
swap(a[i],a[j]);//hoán vị a[i] và a[j]
}
}
}
}
void main()
{
int a[5] = {8, 4, 1, 6, 5};
Interchange_Sort(a, 5);
cout<<"Mang sau khi sap xep:"<<endl;
for(int i=0;i<5;i++){
cout<<a[i]<<" ";
}
system("pause");
}
Kết quả
Mang sau khi sap xep:
1 4 5 6 8Đánh giá giải thuật
Số phép so sánh: Ở mỗi lượt thứ i, luôn có (n-i) lần so sánh a[i]>a[j]. Số lần so sánh là:
Số phép hoán vị tuỳ thuộc vào kết quả so sánh.
Có thể ước lượng trong từng trường hợp như sau:Trường hợp Số lần so sánh Số lần hoán vị Tốt nhất n(n-1)/2 0 Xấu nhất n(n-1)/2 n(n-1)/2
Độ phức tạp thuật toán là O(n2).