Các thao tác trên cây nhị phân tìm kiếm (Binary Search Tree)

1. Đặc điểm của cây nhị phân tìm kiếm

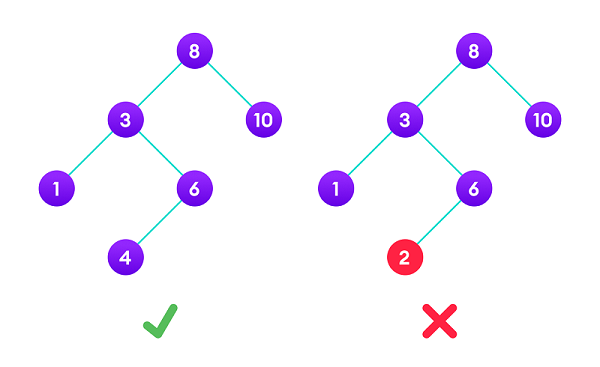
Cây nhị phân tìm kiếm (Binary Search Tree) là một cây nhị phân có đặc điểm:

• • Tất cả các nút trong cây con bên trái lưu trữ giá trị nhỏ hơn nút đang xét
  • Tất cả các nút trong cây con bên phải lưu trữ giá trị lớn hơn nút đang xét

Nhờ trật tự bố trí các nút trên cây giúp định hướng việc tìm kiếm các nút trong cây. Chính vì thế mà nó được gọi là cây nhị phân tìm kiếm.

2. Biểu diễn cây nhị phân tìm kiếm

Chúng ta có thể sử dụng danh sách liên kết để biểu diễn cây nhị phân tìm kiếm. Đầu tiên, cần định nghĩa một nút trong cấu trúc dữ liệu dạng cây.

struct tNode{
	int data;
	tNode *pLeft, *pRight;
};

Dữ liệu (data) lưu trữ trong nút của cây nhị phân tìm kiếm phải là dữ liệu có thể so sánh giá trị nhỏ hơn hoặc lớn hơn giữa các nút trong cây.

Để lưu trữ cây, chúng ta chỉ cần xác định nút gốc của cây.

tNode *root;

Tạo một cây rỗng

void CreateEmptyTree(){
	root = NULL;
}

Tạo một nút lưu giá trị x

tNode *newNode(int data){
	tNode *node = new tNode;
	if(node==NULL){//cannot allocate memory
		exit(1);
	}else{
		node->data = data;
		node->pLeft = NULL;
		node->pRight = NULL;
	}
	return node;
}

3. Các thao tác cơ bản trên cây nhị phân tìm kiếm

Các thao tác trên cây nhị phân tìm kiếm như duyệt cây, thêm một nút vào cây, hủy một nút trong cây, tìm kiếm một nút trong cây,…

Duyệt cây

Cách duyệt giống như cây nhị phân bình thường với 3 kiểu duyệt chính là NLR, LNR, LRN.

Tìm một nút trong cây

Nhờ vào đặc điểm của cây nhị phân tìm kiếm mà việc tìm kiếm nút dễ dàng hơn. Có thể dùng đệ quy hoặc không dùng đệ quy để tìm một nút trong cây nhị phân tìm kiếm.

Sử dụng đệ quy

tNode *searchNodeByRecursion(tNode *root, int x){
	if(root != NULL ){
		if(root->data == x){
			return root;
		}
		if(root->data > x){
			return searchNodeByRecursion(root->pLeft,x);
		}else{
			return searchNodeByRecursion(root->pRight,x);
		}
	}
	return NULL;
}

Không sử dụng đệ quy

tNode *searchNodeWithoutRecursion(tNode *root, int x){
	tNode *p=root;
	while(p != NULL){
		if(p->data == x){
			return p;
		}else if(p->data > x){
			p = p->pLeft;
		}else{
			p = p->pRight;
		}
	}
	return NULL;
}

Thêm một nút vào cây

Sau khi thêm nút vào cây thì đảm bảo vẫn là cây nhị phân tìm kiếm. Lưu ý, không thêm nút lưu giá trị đã có trong cây.

tNode *insertNode(tNode *node, int value){
	if(node!=NULL){
		if(node->data == value){
			return node;
		}else if(node->data > value){
			node->pLeft = insertNode(node->pLeft, value);
		}else{
			node->pRight = insertNode(node->pRight, value);
		}
	}else{
		node = newNode(value);
	}
	return node;
}

Hủy một nút lưu giá trị x trong cây

Khi hủy 1 nút phải đảm bảo điều kiện ràng buộc của cây nhị phân tìm kiếm.

Có 3 trường hợp khi hủy 1 nút trên cây:

Trường hợp 1: x là nút lá. Hủy nút lá mà không ảnh hưởng đến các nút khác trên cây.

Trường hợp 2: x chỉ có 1 cây con (cây con trái hoặc cây con phải). Trước khi hủy x, ta liên kết nút cha của x với con duy nhất của x.

Trường hợp 3: x có đầy đủ 2 cây con. Thực hiện các bước sau để hủy x:

Bước 1: Tìm nút y thế mạng cho nút x, có 2 cách tìm:

• • Cách 1: y là phần tử nhỏ nhất (trái nhất) trên cây con phải.

  • Cách 2: y là phần tử lớn nhất (phải nhất) trên cây con trái.

Bước 2: Lưu thông tin của y vào x.

Bước 3: Hủy y (giống như hủy nút lá).

tNode *minValueNode(tNode *node){
	tNode *current = node;
	while(current && current->pLeft != NULL){
		current = current->pLeft;
	}
	return current;
}

tNode *deleteNode(tNode *root, int x){
	if(root == NULL){
		return root;
	}
	if(root->data > x){
		root->pLeft = deleteNode(root->pLeft, x);
	}else if(root->data < x){
		root->pRight = deleteNode(root->pRight, x);
	}else{
		tNode *p = root;
		if(root->pLeft == NULL){
			root=root->pRight;
			delete p;
		}else if(root->pRight== NULL){
			root=root->pLeft;
			delete p;
		}else{
			tNode *temp = minValueNode(root->pRight);
			root->data = temp->data;
			root->pRight = deleteNode(root->pRight, temp->data);
		}
	}
	return root;
}

4. Ví dụ chương trình C++ thao tác với cây nhị phân tìm kiếm

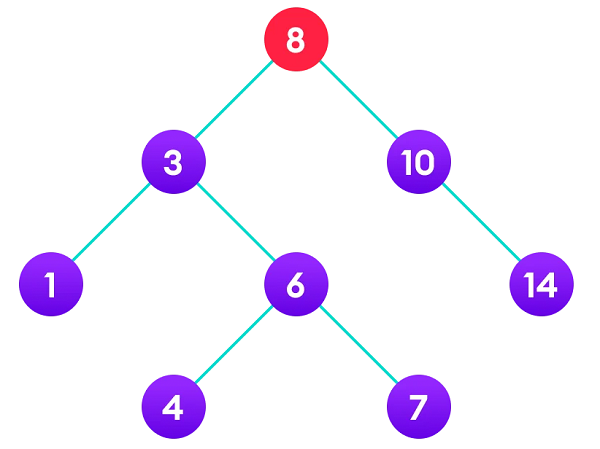
Cho cây nhị phân tìm kiếm như hình bên dưới.

Chương trình C++ thao tác với cây nhị phân tìm kiếm như hình trên

#include <iostream>
using namespace std;

struct tNode{
	int data;
	tNode *pLeft, *pRight;
};

tNode *root;

//create empty tree
void createEmptyTree(){
	root = NULL;
}

//create new node
tNode *newNode(int data){
	tNode *node = new tNode;
	if(node==NULL){//cannot allocate memory
		exit(1);
	}else{
		node->data = data;
		node->pLeft = NULL;
		node->pRight = NULL;
	}
	return node;
}

//insert new Node into tree
tNode *insertNode(tNode *node, int value){
	if(node!=NULL){
		if(node->data == value){
			return node;
		}else if(node->data > value){
			node->pLeft = insertNode(node->pLeft, value);
		}else{
			node->pRight = insertNode(node->pRight, value);
		}
	}else{
		node = newNode(value);
	}
	return node;
}

void NLR(tNode *root){
	if(root!=NULL){
		if(root!=NULL){
			cout<<root->data<<" ";
		}
		NLR(root->pLeft);
		NLR(root->pRight);
	}
}

tNode *searchNodeByRecursion(tNode *root, int x){
	if(root != NULL ){
		if(root->data == x){
			return root;
		}
		if(root->data > x){
			return searchNodeByRecursion(root->pLeft,x);
		}else{
			return searchNodeByRecursion(root->pRight,x);
		}
	}
	return NULL;
}

tNode *searchNodeWithoutRecursion(tNode *root, int x){
	tNode *p=root;
	while(p != NULL){
		if(p->data == x){
			return p;
		}else if(p->data > x){
			p = p->pLeft;
		}else{
			p = p->pRight;
		}
	}
	return NULL;
}

tNode *minValueNode(tNode *node){
	tNode *current = node;
	while(current && current->pLeft != NULL){
		current = current->pLeft;
	}
	return current;
}

tNode *deleteNode(tNode *root, int x){
	if(root == NULL){
		return root;
	}
	if(root->data > x){
		root->pLeft = deleteNode(root->pLeft, x);
	}else if(root->data < x){
		root->pRight = deleteNode(root->pRight, x);
	}else{
		tNode *p = root;
		if(root->pLeft == NULL){
			root=root->pRight;
			delete p;
		}else if(root->pRight== NULL){
			root=root->pLeft;
			delete p;
		}else{
			tNode *temp = minValueNode(root->pRight);
			root->data = temp->data;
			root->pRight = deleteNode(root->pRight, temp->data);
		}
	}
	return root;
}

int main()
{
	//create binary search tree
	createEmptyTree();
	root = insertNode(root, 8);
	root = insertNode(root, 3);
	root = insertNode(root, 1);
	root = insertNode(root, 6);
	root = insertNode(root, 7);
	root = insertNode(root, 10);
	root = insertNode(root, 14);
	root = insertNode(root, 4);
	cout<<"traverse tree with NLR:";
	NLR(root);
	tNode *temp = searchNodeWithoutRecursion(root, 10);
	if(temp!=NULL){
		cout<<endl<<"Found x=10";
	}else{
		cout<<endl<<"Cannot found x=10";
	}
	root = deleteNode(root, 3);
	cout<<endl<<"traverse tree with NLR after delete node:";
	NLR(root);
	system("pause");
}

Kết quả

traverse tree with NLR:8 3 1 6 4 7 10 14
Found x=10
traverse tree with NLR after delete node:8 4 1 6 7 10 14