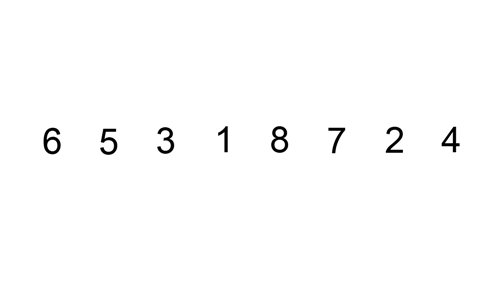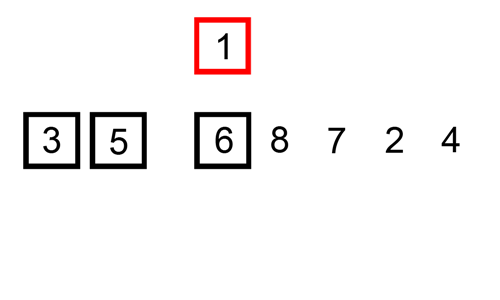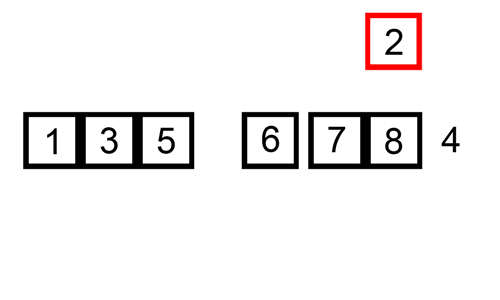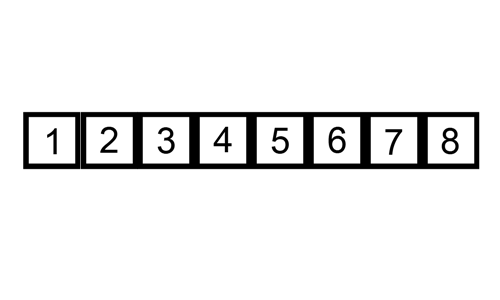1. Ý tưởng thuật toán sắp xếp chèn trực tiếp
Giả sử cần sắp xếp tăng dần một danh sách có n phần tử a0, a1, a2,…,an-1.
Giả sử đoạn a[0] trong danh sách đã được sắp xếp. Bắt đầu từ phần tử thứ i=1, tức là a1. Tìm cách chèn phần tử ai vào vị trí thích hợp của đoạn đã được sắp xếp để có dãy mới a0,…,ai trở nên có thứ tự. Vị trí này chính là vị trí giữa hai phần tử ak-1 và ak thỏa ak-1 < ai < ak (0<= k <=i). Lưu ý, khi k=0 thì có nghĩa là ai cần chèn vào trước vị trí đầu tiên trong danh sách.
Lặp lại quá trình trên ở mỗi lần lặp với mỗi lần lặp thì tăng i lên 1 đến khi i<n thì dừng quá trình lặp.
Một câu hỏi đặt ra là cách chèn phần tử trong danh sách như thế nào? Các bạn hãy đọc tiếp phần 2 và 3 nhé.
2. Các bước thực hiện thuật toán
Bước 1: i = 1;//giả sử có đoạn a[0] đã được sắp xếp
Bước 2: x = a[i];
Bước 3:
Tìm vị trí pos thích hợp trong đoạn a[0] đến a[i-1] để chèn a[i] vào danh sách.
Dời chỗ các phần tử từ a[pos] đến a[i-1] sang phải 1 vị trí để dành chổ cho a[i].
Bước 4: a[pos] = x;//chèn x, có đoạn a[0],…,a[i] đã được sắp.
Bước 5: i = i+1; nếu i < n -> lặp lại bước 2, ngược lại -> Dừng.
Minh họa thuật toán sắp xếp chèn trực tiếp
3. Cài đặt thuật toán sắp xếp chèn trực tiếp với C++
void Insertion_Sort(int a[], int n){
int pos, i;
int x;//lưu giá trị a[i] tránh bị ghi đè khi dời chỗ các phần tử
for(i=1; i<n; i++){//đoạn a[0] đã sắp xếp
x = a[i]; pos = i-1;
//tìm vị trí chèn x
while((pos>=0)&&(a[pos]>x)){
//kết hợp dời chỗ các phần tử sẽ đứng sau x trong danh sách mới
a[pos+1] = a[pos];
pos--;
}
a[pos+1] = x;//chèn x vào danh sách
}
}
void main()
{
int a[5] = {8, 4, 1, 6, 5};
Insertion_Sort(a, 5);
cout<<"Mang sau khi sap xep:"<<endl;
for(int i=0;i<5;i++){
cout<<a[i]<<" ";
}
system("pause");
}Kết quả
Mang sau khi sap xep:
1 4 5 6 8
Đánh giá thuật toán
| Trường hợp | Số lần so sánh |
| Tốt nhất | n-1 |
| Xấu nhất | n(n-1)/2 |
Độ phức tạp thuật toán trong trường hợp xấu nhất là O(n2).