1. Thuật toán tìm kiếm nhị phân
Tìm kiếm nhị phân được áp dụng trên các danh sách đã được sắp xếp theo thứ tự. Giả sử, có mảng a0,a1,a2,..,an-1 đã được sắp xếp theo thứ tự tăng dần. Các phần tử trong dãy có mối quan hệ: ai -1 ≤ ai ≤ ai+1.
Ý tưởng thuật toán
Nếu x > ai thì x chỉ có thể xuất hiện trong đoạn [ai+1, an-1].
Nếu x < ai thì x chỉ có thể xuất hiện trong đoạn [a0, ai-1].
Tại mỗi bước, ta so sánh x với phần tử đứng giữa trong mảng đang tìm kiếm, dựa vào kết quả so sánh này mà ta quyết định giới hạn dãy tìm kiếm ở nữa dưới hay nữa trên của dãy tìm kiếm hiện hành.
Các bước thực hiện thuật toán
Giả sử mảng tìm kiếm hiện hành bao gồm các phần tử nằm trong aleft, aright. Các bước của giải thuật như sau:
Bước 1: Gán left=0; right=n-1;
Bước 2:
mid=(left+right)/2;//chỉ số phần tử giữa mảng hiện hành
So sánh a[mid] với x. Có 3 khả năng:
- a[mid] == x -> tìm thấy -> Dừng.
- a[mid] > x thì gán right=mid-1;//tìm tiếp x trong mảng con a[left],..,a[mid-1]
- a[mid] < x thì gán left=mid+1;//tìm tiếp x trong mảng con a[mid+1],..,a[right]
Bước 3: Nếu left <= right; thì lặp lại bước 2. Ngược lại thì dừng.
Minh họa thuật toán
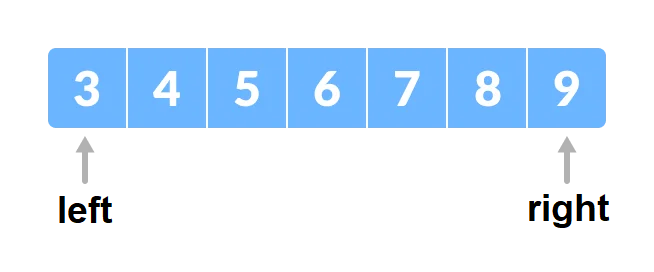
Tìm x=4 trong mảng đã được sắp xếp tăng dần bên dưới.
Xác định left=0 và right=6 trên mảng đang xét.
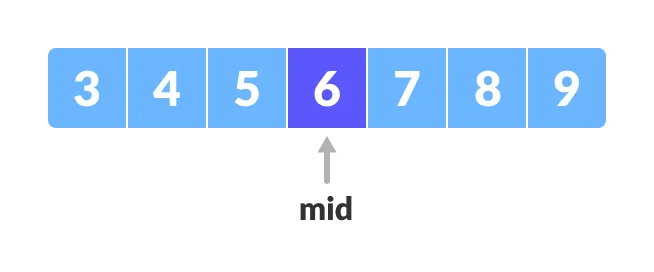
Xác định được mid=(left+right)/2=3 trong mảng đang xét và a[mid]=6.
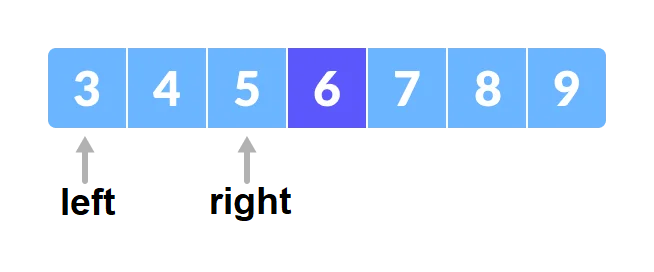
Giá trị x=4 nhỏ hơn a[mid]=6 nên right=mid-1=2, left vẫn là 0. Mảng con đang xét hiện giờ là a[left],…,a[right].
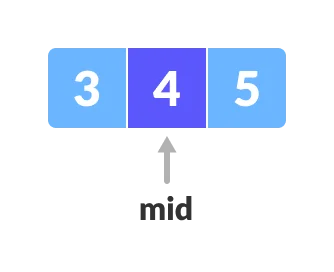
Xác định lại mid=(left+right)/2=1 và a[mid]=4.
Tìm được x=4 trong mảng con.
Đánh giá thuật toán tìm kiếm nhị phân
| Trường hợp | Số lần so sánh | Giải thích |
| Tốt nhất | 1 | Phần tử giữa của mảng có giá trị x |
| Xấu nhất | log2n | Không có x trong mảng |
| Trung bình | log2(n/2) | Xác suất các phần tử trong mảng nhận giá trị x là như nhau |
Độ phức tạp của thuật toán là O(log2n).
Cài đặt thuật toán tìm kiếm nhị phân với C++
Hàm BinarySearch() trả về mid là vị trí của x trong mảng nếu tìm thấy x, ngược lại hàm trả về giá trị -1.
int BinarySearch(int a[],int n,int x)
{
int left, right, mid; left=0; right=n-1;
do{
mid=(left+right)/2;
if(a[mid]==x){
return mid;
}
else if(a[mid]<x){
left=mid+1;
}
else{
right=mid-1;
}
}while(left<=right);
return -1;
}
2. Cài đặt thuật toán tìm kiếm nhị phân dùng đệ quy
Dễ thấy, thuật toán tìm kiếm nhị phân là sự lặp đi lặp lại của quá trình xác định mid và so sánh a[mid] có bằng giá trị x cần tìm trong mảng hay không. Ta có thể viết một hàm làm nhiệm vụ đó rồi gọi lại chính nó để cài đặt thuật toán. Đó chính là kỹ thuật lập trình đệ quy đã học ở môn Nhập môn lập trình.
int BinarySearch_Recursive(int a[],int x,int left,int right){
if(left>right){
return -1;
}
int mid=(left+right)/2;
if(x==a[mid]){
return mid;
}
if(x<a[mid]){
return BinarySearch_Recursive(a,x,left,mid-1);
}
return BinarySearch_Recursive(a,x,mid+1,right);
}
3. Phân tích và so sánh các thuật toán tìm kiếm
Sau khi tìm hiểu thuật toán tìm kiếm tuyến tính và tìm kiếm nhị phân (binary search), chúng ta có một số phân tích sau:
– Thuật toán binary search tiết kiệm thời gian hơn rất nhiều so với tìm kiếm tuyến tính.
– Thuật toán binary search chỉ được áp dụng cho những mảng đã được sắp xếp thứ tự. Thuật toán tìm kiếm tuyến tính áp dụng cho bất kỳ mảng nào cũng được.
– Khi sử dụng thuật toán binary search cần tính đến chi phí sắp xếp. Khi mảng có sự thay đổi các phần tử như thêm, xóa,… thì phải sắp xếp lại. Đây là khuyết điểm chính của thuật toán binary search.


![Tìm thấy x = a[mid]](https://gochocit.com/wp-content/uploads/2021/10/binary-search-found.png)



Cho hỏi nếu tìm nhị phân trên danh sách liên kết đơn thì có hiệu quả không ạ?
:)))