1. Cấu trúc dữ liệu là gì?
Cấu trúc dữ liệu (data structure) là cách thức tổ chức dữ liệu sao cho phù hợp với bài toán và có thể dùng máy tính để xử lý các dữ liệu đó một cách hiệu quả.
Các tiêu chuẩn của một cấu trúc dữ liệu:
- Phải biểu diễn đầy đủ thông tin
- Phải phù hợp với các thao tác xử lý
- Phù hợp với điều kiện cho phép của ngôn ngữ lập trình
- Tiết kiệm được tài nguyên hệ thống
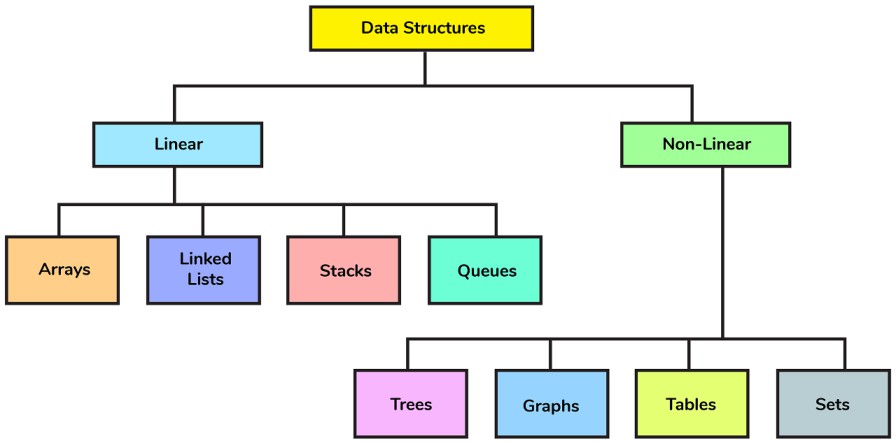
Có nhiều loại cấu trúc dữ liệu nhưng có thể chia thành 2 loại: cấu trúc dữ liệu tuyến tính (linear) và phi tuyến tính (non-linear).
2. Giải thuật là gì?
Giải thuật là tên gọi khác của thuật toán. Thuật toán (algorithm) là tập hợp hữu hạn các thao tác được định nghĩa rõ ràng nhằm giải quyết một bài toán cụ thể nào đó.
Một thuật toán phải đảm bảo 5 tính chất sau:
– Tính chính xác: quá trình tính toán hay các thao tác máy tính thực hiện là chính xác.
– Tính rõ ràng: các câu lệnh minh bạch được sắp xếp theo thứ tự nhất định.
– Tính khách quan: được viết bởi nhiều người trên máy tính nhưng kết quả phải như nhau.
– Tính phổ dụng: có thể áp dụng cho một lớp các bài toán có đầu vào tương tự nhau.
– Tính kết thúc: hữu hạn các bước tính toán.
Các bạn có thể đọc thêm bài Thuật toán là gì? Các phương pháp biểu diễn thuật toán để hiểu rõ hơn về thuật toán.
3. Mỗi liên hệ giữa cấu trúc dữ liệu và giải thuật
Thuật toán và cấu trúc dữ liệu có mối quan hệ chặt chẽ với nhau. Cuốn sách “Algorithms + Data Structures = Programs” là một trong những cuốn sách kinh điển của nhà khoa học máy tính Niklaus Wirth viết vào năm 1976 nói lên điều đó.
Thật vậy, bất kỳ một chương trình nào cũng cần có dữ liệu để tính toán, xử lý. Nhiệm vụ tính toán, xử lý sẽ được giao cho thuật toán. Để chương trình hoạt động tốt, ổn định thì thuật toán phải xử lý tốt và chính xác trên dữ liệu. Do đó, những dữ liệu này cần được lưu trữ, tổ chức một cách hợp lý với thuật toán.
Rõ ràng, cấu trúc dữ liệu đóng vai trò quan trọng trong việc kết hợp và đưa ra cách giải quyết bài toán. Cấu trúc dữ liệu cũng hỗ trợ cho các thuật toán thao tác, xử lý hiệu quả hơn.
4. Độ phức tạp thuật toán
Với một bài toán, chúng ta có thể có nhiều thuật toán để giải quyết bài toán đó. Nhưng một câu hỏi đặt ra là thuật toán nào tốt hơn thuật toán nào? Để trả lời câu hỏi này, cần xem xét thế nào là một thuật toán hiệu quả?
Một thuật toán hiệu quả thì chi phí sử dụng tài nguyên như bộ nhớ, thời gian sử dụng CPU,… thấp. Người ta thường phân tích độ phức tạp thuật toán để đánh giá sự hiệu quả của thuật toán. Có hai phương pháp đánh giá độ phức tạp của thuật toán là:
- Phương pháp thực nghiệm
- Phương pháp xấp xỉ toán học
Phương pháp thực nghiệm
Cài thuật toán rồi chọn các bộ dữ liệu thử nghiệm. Chạy thuật toán rồi thống kê các thông số (thời gian chạy thuật toán, dung lượng bộ nhớ,…) khi chạy thuật toán với các bộ dữ liệu đó.
Ưu điểm: Dễ thực hiện.
Nhược điểm:
- Chịu sự hạn chế của ngôn ngữ lập trình
- Ảnh hưởng bởi trình độ của người lập trình
- Chọn được các bộ dữ liệu thử đặc trưng cho tất cả tập các dữ liệu đầu vào của thuật toán thì khó khăn và tốn nhiều chi phí
- Phụ thuộc vào phần cứng
Trong nghiên cứu khoa học, phương pháp này được sử dụng rất nhiều.
Phương pháp xấp xỉ toán học
Đánh giá độ phức tạp thuật toán theo hướng xấp xỉ tiệm cận qua các khái niệm O(). Hiểu đơn giản là xấp xỉ số lần thực hiện các phép toán của thuật toán. Số lần thực hiện phép toán càng ít thì thuật toán càng ít phức tạp (càng tốt) và ngược lại.
Ưu điểm: Ít phụ thuộc ngôn ngữ lập trình cũng như phần cứng hơn.
Nhược điểm: Cách tính phức tạp, cần có kiến thức toán học.
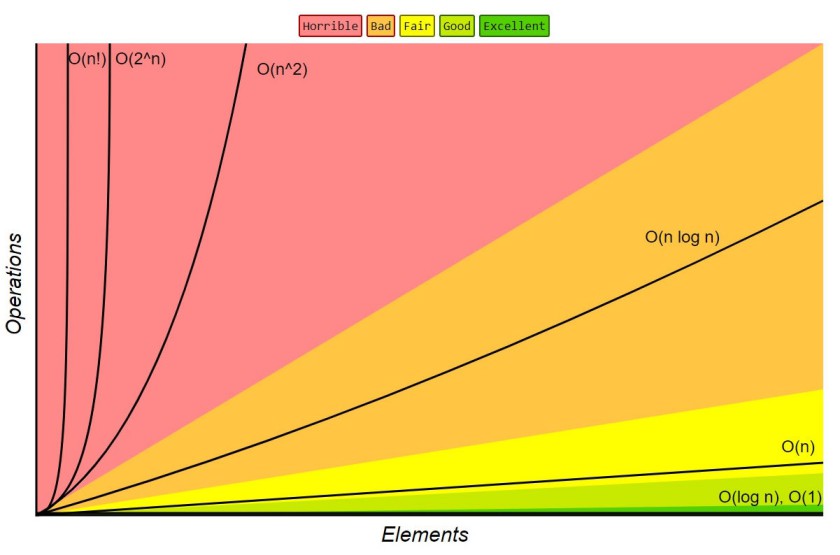
Người ta sử dụng các ký hiệu BigO bên dưới để đánh giá độ phức tạp thuật toán theo độ phức tạp tăng dần.
- Hằng số: O(c)
- logN: O(logN)
- N: O(N)
- NlogN: O(NlogN)
- N2: O(N2)
- N3: O(N3)
- 2N: O(2N)
- N!: O(N!)
Một số ví dụ về độ phức tạp thuật toán
Ví dụ 1:
for (int i=1;i<=n;i++) {
x=x+1;
}
thực hiện n lần phép toán, độ phức tạp thuật toán là O(n).
Ví dụ 2:
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++ ){
x=x+1;
}
}
thực hiện n*n lần phép toán, độ phức tạp thuật toán là O(n2).