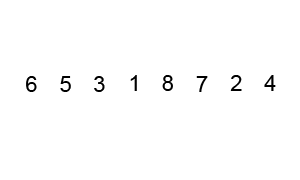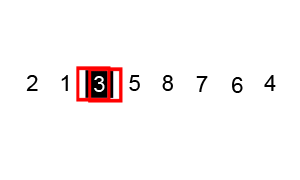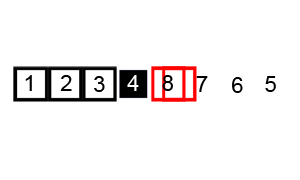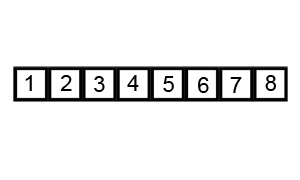1. Ý tưởng thuật toán sắp xếp Quick Sort
Giả sử cần sắp xếp tăng dần một danh sách có n phần tử a0, a1, a2,…,an-1.
Đầu tiên chọn tuỳ ý phần tử x trong danh sách làm mốc (thường chọn là phần tử giữa danh sách).
Ý tưởng của thuật toán Quick Sort phân hoạch danh sách ban đầu thành 3 phần:
Phần 1: Gồm các phần tử có giá trị bé hơn x.
Phần 2: Gồm các phần tử có giá trị bằng x.
Phần 3: Gồm các phần tử có giá trị lớn hơn x.
Sau khi thực hiện phân hoạch, danh sách ban đầu được phân thành 3 đoạn:
1. ak < x, với k = 0…i
2. ak = x, với k = i+1…j-1
3. ak > x, với k = j…n-1
Lúc này, đoạn thứ 2 đã có thứ tự. Nếu các đoạn 1 và 3 chỉ có 1 phần tử thì coi như danh sách ban đầu đã được sắp xếp.
Nhưng nếu các đoạn 1 và 3 có nhiều hơn 1 phần tử thì danh sách ban đầu chỉ có thứ tự khi các đoạn 1, 3 được sắp xếp.
Để sắp xếp các đoạn 1 và 3, ta lần lượt tiến hành việc phân hoạch từng đoạn con 1 và 3 theo cùng phương pháp phân hoạch danh sách ban đầu vừa trình bày.
Đến đây, các bạn sẽ thắc mắc cách phân hoạch danh sách như thế nào phải không? Hãy đọc tiếp phần 2 nhé.
2. Các bước thực hiện thuật toán
Bước 1: Gán left là vị trí đầu danh sách bên trái, right là vị trí đầu danh sách bên phải.
Bước 2: Nếu left >= right thì kết thúc (danh sách chỉ có 1 phần tử). Ngược lại thì:
Bước 2.1: Chọn tùy ý một phần tử a[k] trong danh sách (left <= k <= right): x=a[k]; i=left; j=right;
Bước 2.2: Tìm kiếm và đổi chổ cặp phần tử a[i], a[j] nằm sai chổ
Trong khi (a[i]<x) i++;
Trong khi (a[j]>x ) j- -;
Nếu i<=j thì đổi chổ a[i], a[j].
i++; j- -;
Bước 2.3: Nếu i<=j thì lặp lại bước 2.2.
Bước 3:
Nếu left<j thì gọi đệ quy để phân hoạch danh sách con a[left],…,a[j].
Nếu i<right thì gọi đệ qui để phân hoạch danh sách con a[i],…,a[right].
Minh họa thuật toán Quick Sort
3. Cài đặt thuật toán sắp xếp Quick Sort với C++
#include <iostream>
using namespace std;
void Quick_Sort(int a[], int left, int right){
int i, j, x;
x = a[(left+right)/2];
i = left; j = right;
do{
while(a[i] < x) i++;
while(a[j] > x) j--;
if(i <= j){
swap(a[i],a[j]);
i++; j--;
}
}while(i <= j);
if(left<j){
Quick_Sort(a, left, j);
}
if(i<right){
Quick_Sort(a, i, right);
}
}
void main()
{
int a[5] = {8, 4, 1, 6, 5};
Quick_Sort(a, 0, 4);
cout<<"Mang sau khi sap xep:"<<endl;
for(int i=0;i<5;i++){
cout<<a[i]<<" ";
}
system("pause");
}
Kết quả
Mang sau khi sap xep:
1 4 5 6 8
Đánh giá giải thuật
| Trường hợp | Số lần so sánh |
| Tốt nhất | O(nlog(n)) |
| Trung bình | O(nlog(n)) |
| Xấu nhất | O(n2) |
Độ phức tạp thuật toán trong trường hợp trung bình là O(nlog(n)). Trong trường hợp xấu nhất là O(n2) như các thuật toán Interchange Sort, Selection Sort, Bubble Sort. Nhưng người ta kỳ vọng nếu danh sách cần sắp xếp chỉ rời vào trường hợp trung bình và tốt nhất thì chi phí sắp xếp sẽ giảm đi rất nhiều, tốt hơn các thuật toán khác. Đó là lý do mà thuật toán này có tên là Quick Sort.